17a
Olitele (Concurs telemàtic SCM.
curs 23-24)
Problema 11, la darrera proposta del concurs (que atorga
un màxim de 7
punts)
Cal enviar una explicació
detallada d'un raonament que porti a la solució del problema
Molt important
Abans d'enviar la resposta al aquest problema
llegiu si us plau, les consideracions
generals sobre els problemes "d'explicar"
En aquest problema demanem que reflexioneu pel que fa a una figura com aquesta:
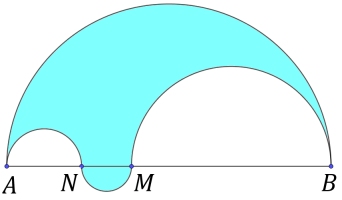
En un semicercle de diàmetre AB s'ha marcat un punt M de manera que la ditància AM = d i un punt N en el segment AM (el punt N és diferent de A i de M) i aleshores s'han traçat els semicercles de diàmetres respectius AN, NM i MB i s'ha acolorit l'àrea que podeu veure.
Naturalment la imatge és només orientativa i les mesures dels tres semicercles poden ser diverses segons les longituds de AM i NB.
a) Si es compleix que AM = d i que NB = 2d, calculeu, en funció de d, l'àrea S de la zona acolorida. En aquesta mateixa situació, si T és la superfície del semicercle de diàmetre AB, raoneu entre quins valors pot variar la raó r = S/T. (es demana el límit inferior i el límit superior: nombres que enacara que r no els pugui assolir, s'hi pugui acostar tant com es vulgui)
b) Ara estudiarem el cas general amb AM = d i NB = b. Raoneu quines parelles de nombres enters positius (d, b) tenen la propietat que es pot fer la construcció de la figura del problema de manera que els radis dels quatre semicercles que hi
apareixen siguin nombres enters positius i que l'àrea acolorida és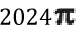 
. Digueu també quantes són les parelles que compleixen la propietat indicada.
- D'aquest problema has d'enviar un fitxer .PDF on hi hauràs escrit
ben clarament la solució del problema i,
tan detallat com sigui possible, i alhora precís, un camí de raonament
que porti a la solució indicada.
El format inicial del document pot ser el que et vagi millor (LaTeX,
Word, OpenOffice, o fins i tot a mà escanejat) però hauràs de
convertir-lo a .PDF. Hi ha programari lliure que permet fer la
conversió
- Només es pot fer una tramesa de solució d'aquest problema.
- Com sempre, el formulari per enviar la solució es
trobarà a
la pàgina índex de l'activitat.
Consideracions
sobre els problemes "d'explicar"
Previ: El
concurs es proposa com una activitat
individual per
a alumnes dels
nivells
indicats. És clar que la comissió organitzadora també valora
molt positivament que les propostes de problemes serveixin per al
treball en equip. Tanmateix, a l'hora de redactar el raonament que
porta a la solució del problema és imprescindible que en la redacció i
la presentació s'observi una tasca individual. Sent així, si dos
concursants envien el mateix fitxer PDF no entrarà en
consideració per a l'avaluació. Quan dues persones, sense copiar
textualñment,
redacten la solució a un problema sempre hi haurà aspectes que
diferenciaran una explicació de l'altra, encara que abans ho hagin
comentat entre elles.
Sobre l'avalaució dels problemes "d'explicar" i l'assignació de
puntuacions
- Cadascun
dels problemes l'avaluaran quatre o cinc persones,
professores o professors universitaris o de secundària, en actiu o
jubilats. A partir dels criteris generals que s'apliquen en concursos
de resolució de problemes matemàtics, cada persona aporta el seu propi
punt de vista i posa la seva puntuació. Després es fa la mitjana de
puntuacions i s'arronodeix, cap a dalt, al primer decimal.
- Per als criteris d'avaluació es té en compte
com a idees bàsiques:
- Cal
redactar ben clarament la
solució del problema i, tan detallat
com sigui possible, i alhora precís, un camí de raonament
que porti a la solució indicada.
- L'absència
total o molt accentuada de redacció (cosa que es pot observar en
determinades respostes si es fa "Només" us de recursos del
sotware informàtic disponible) s'entèn que no s'adiu amb la indicació
anterior. Així mateix una excessiva faramalla en els prolegòmens de
l'explicació o l'ús de recursos excessivament sofisticats es pot
entendre com una pèrdua de precisió.
- Hem
de pensar que aquestes respostes s'envien a un concurs, que és una
situació ben diferent d'un "examen escolar". És a dir que si dos
participants fan raonaments semblants, però un ho explica de manera més
completa, concreta i precisa que l'altre, o amb raonaments
conceptualment més interessants, la comissió avaluadora
tindrà una tendència a posar-li més punts. En aquest sentit podem
afegir que la subtil diferència entre un 6,8 o un 6,9 o un 7 es
pot considerar una diferència de puntuació "a efectes de desempats", i
que en concursos com aquest una puntuació de 6 o més ja s'ha de
considerar una valoració ben bona.