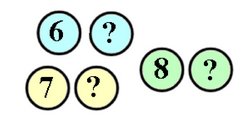amb el suport de  
Marató de problemes. 2021
Problema 8, problema de 7 punts

Malgrat que la proposta es puntua de 0 a 7 punts, el jurtat es reserva la possibilitat d'atorgar 1 o 2 dècimes suplementàries per a respostes i raonaments que ho facin aconsellable

D'aquest problema se'n fa una presentació guiada;  caldrà enviar la solució raonada de cada apartat,
i explicada amb detall però amb precisió, sense explicacions innecessàries en un fitxer .PDF.
 El format original del document amb  l'explicació pot ser el que vulguis -fins i tot escanejar un escrit a mà- però l'has de passar al format .PDF i vigilar que es llegeixi adequadament

Aquest concurs vol fomentar l'afició per al treball matemàtic mitjançant la resolució de problemes
i, naturalment, tot i que el concurs és individual, el treball en equip sempre pot tenir un valor afegit.
Ara bé, encara que hi hagi hagut una tasca conjunta, és imprescindible que
la redacció de la solució d'aquesta proposta sigui una tasca personal, individual.

La repsosta s'haurà d'enviar mitjançant un formulari, que, com és habitual, serà accessible des de la pàgina de l'activitat.

Tenim un conjunt de cartes rodones que tenen escrit un nombre enter positiu en cadascuna de les dues cares. 
N'agafem algunes, les tirem enlaire, i sumem els nombres que marquen les cares que queden mirant amunt.
Per exemple,  si ho fem amb dues cartes, una amb un 1 i un 2, i l'altra amb un 6 i un 8,  les sumes que podem obtenir són 7, 8, 9 i 10. Vegeu-ho: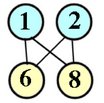
A)
Ara agafem dues cartes i veiem  per per una cara tenen el 3 i el 9.
Si ens diuen que les sumes que es poden obtenir són 8, 11, 12 i 15, quines són les dues cartes?  Cal que expliquis com ho veus i que estudiïs totes les possibilitats.
B)
En l'exemple anterior que hem donat els quatre nombres que es poden obtenir són quatre nombres enters consecutius. Hi ha altres parelles de cartes que també donen les mateixes sumes 7, 8, 9, i 10.  Raona quines són aquestes altres parelles de cartes  i generalitza-ho per a deduir quines són totes les parelles d ecartes que poden donar com a sumes els quatre nombres enters consecutius a, a+1, a+2 i a+3.
C)
Ara agafem tres cartes que per una cara tenen escrits els nombres 6, 7 i 8.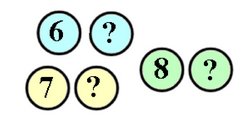
Raona quines són totes les possibilitats dels nombres que es troben escrits al darrere de cada carta si els resultats que es poden obtenir com a suma dels tres números que queden a dalt, de les vuit possibles maneres que poden quedar les cartes, són  15, 16, 17, 18, 20, 21, 22, 23.
D)
 És possible que, amb tres cartes, les vuit sumes possibles resultin ser vuit nombres enters consecutius?
Com en tots els apartats cal que donis un raonament  i que estudiïs totes les possibilitats.


Notes: 
  • Cal redactar ben clarament la solució de cada apartat del problema i, tan detallat com sigui possible, i alhora precís, un camí de raonament que porti a especificar que  la solució és la indicada, amb la indicació de totes les possibilitats
  • Heu de pensar que aquestes respostes s'envien a un concurs, que és una situació ben diferent a la d'un "examen escolar". És a dir que si dos participants fan raonaments semblants, però un ho explica de manera més completa, concreta o precisa que l'altre, o amb alguna idea original,  la comissió avaluadora tindrà una tendència a posar-li més punts. En aquest sentit podem afegir que  la subtil diferència entre un 6,8 o un 6,9 o un 7 es pot considerar una diferència de puntuació "a efectes de desempats".
  • Cada resposta la valoraran un cert nombre de persones (del món de l'enseyament secundari o universitari), de manera que cada una aportarà el seu punt de vista i es farà una mitjana de les puntuacions atorgades.
  • El diccionari defineix  precís com Exactament o estrictament determinat o definit, no equívoc o vague.  Si l'explicació és enrevessada, o ampul·losa, això pot ser considerat pèrdua de precisió i de concreció i, per tant, pot influir en la valoració. La presentació de diversos camins de solució que no aportin idees creatives essencialment diferents també pot ser considerat com una pèrdua dc concreció o de precisió.

  • Ja sabeu que podeu elevar consultes a la comissió del concurs:   concursosscm@gmail.com