amb el suport de  
Marató de problemes. 2017
Problema 15. L'últim problema!  (de 7 punts)

Malgrat que el problema es puntua de 0 a 7 punts, el jurtat es reserva la possibilitat d'atorgar 1 o 2 dècimes suplementàries per a respostes i raonaments que ho facin aconsellable
D'aquest problema caldrà enviar la solució raonada i explicada amb detall, rigor i concreció en un fitxer .PDF.
Quan ja hagis resolt el problema hauràs d'accedir al formulari, que està accessible des de la pàgina de l'activitat.
  1. ABC és un triangle rectangle isòsceles que té els costats iguals de 4 cm.  Calcula l'àrea de la regió formada per tots els punts P interiors al triangle ABC  des dels quals els tres angles amb què es veuen els costats del triangle (és a dir els angles APB, BPC i CPA) són tots tres obtusos.
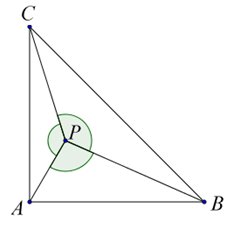    La figura mostra un dels punts que compleixen l'enunciat

  2. Descriviu quina és, en general, la regió formada per tots els punts interiors a un triangle qualsevol des dels quals els tres angles amb què es veuen els costats del triangle  són tots tres obtusos. 
    (en aquest cas general no es demana que en calculeu l'àrea, només  que descriviu la regió "en general", és a dir segons les característiques de cada "triangle qualsevol" que interessi estudiar de manera diferenciada.)

La valoració dels apartats a i b és, respectivament,  de 4 i 3 punts
Reproduïm un paràgraf d'un escrit publicat a la pàgina principal del concurs:  si els càlculs que es demanen s'expliquen bé, però concisament, ajudaran a donar més punts; si es fa servir un mètode més "elegant" que un altre també pot donar més punts, si s'aprofiten els resultats d'un apartat per a un altre, això pot ser molt ben valorat. En aquest cas, on diu "càlculs"  llegiu-hi per al segon apartat "descripcions de la regió, segons el tipus de triangle".