|
Molt
bé! ¡Muy
bien! Moi ben!
¡Todas
las respuestas
correctas! Por si os queda tiempo, ahora os proponemos nuevos
retos.
Podéis enfrentaros a ellos en el orden que queráis.
Problema
1 "de propina"
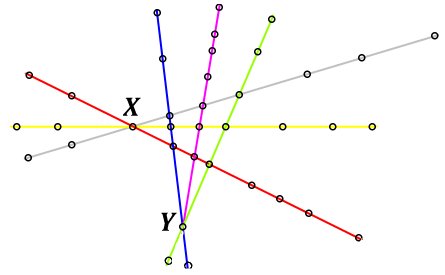
La figura
muestra el mapa de las seis líneas de metro de la ciudad de
Estalmat. Los puntos representan las estaciones y en todas
aquellas donde se cruzan dos o más líneas se puede cambiar de una a
otra.
Juliana quiere viajar de la estación X a la estación Y sin usar una
línea de metro más de una vez (y sin volver a la estación X ni salir de la
estación Y
cuando ya haya llegado a ella).
¿Cuántos itinerarios siguientes puede escoger, sin preocuparse que sean
lo más cortos posible, pero cumpliendo las condiciones indicadas?
|
|
Problema
2 "de propina"
|
Cuál es el menor valor que puede tener n para que las seis
fracciones propias
se puedan simplificar?
(Nota: deben ser m, n enteros
positivos con m < n, es
decir que se podrá escribir n = m+a,
siendo a un número entero
positivo)
|
Problema
3 "de propina"
Hemos
"aprisionado" un hexágono regular de lado 2 entre su círculo inscrito y
su círculo circunscrito. Lo mismo hemos hecho con un heptágono regular
de lado 2.
Si H6 es el área de la corona
circular que aprisiona el hexágono y H7 la de
la corona circular que aprisiona el heptágono, entonces H7 – H6 se
puede escribir como
a·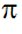 siendo a un número racional. ¿Cuál es el valor de a? siendo a un número racional. ¿Cuál es el valor de a?
|
|