|
Problemes
a l'esprint - SCM- edu365
2 de febrer de 2006
Tot seguit comentem
algunes idees per a obtenir les solucions i obrim "un fòrum".
Si voleu enviar alguna nova solució dels alumnes participants
(segur que elles i ells n'han trobar de millors!) no dubteu a
enviar-les a esprint@cangur.org
i ampliarem el "fons d'idees".
Respostes comentades
- Problemes de la
branca d'olivera
- 1. B.
Cal recordar quant sumen els angles d'un
polígon. Tots els angles d'un polígon de 12
costats sumen 180º·10, els d'un de 13 sumen
180º·11, els d'un de 14 sumen 180º·12=
2160º, etc. Com que en un polígon còncau
tots els angles han de ser més petits de 180º,
el polígon ha de ser de 14 costats.
- 2. E.
El total de participants és x +
x/2 + x/6 = 10x/6. Perquè cadascun dels sumands x,
x/2, x/6 sigui un nombre natural., x ha de ser un múltiple
de 6. I llavors el total de participants ha de ser múltiple
de 10.
- 3. E.
El radi del sector ha de ser la generatriu
del con. La longitud del sector, que és 252·2
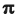 ·10/360
ha de ser la longitud del cercle base del con. Si igualeu
l'expressió anterior a 2 ·10/360
ha de ser la longitud del cercle base del con. Si igualeu
l'expressió anterior a 2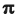 r
veureu que ha de ser r = 7. r
veureu que ha de ser r = 7.
- 4. A.
Si poseu William Jones al Google la primera
pàgina que apareix a la lista és la de la
Universitat de Saint Andrews, una de les webs de més
prestigi pel que fa a la història de les matemàtqiues
- 5. D.
Si estudieu el problema veureu que
el color roig apareix 2·(1+5+9+13+17+21+25+29+33+37+41)+45
vegades. Aquest valor és K.
Els altres color apareixen el mateix nombre de vegades,
per exemple el verd 2+6+10+14+18+22+26+30+34+38+42+44 (seria
"la línia 46, però aquí ja comença
a baixar la longitud de les inclinades) + 40+36+32+28+24+20+16+12+8+4.
Aquest valor és k. I es compleix que K–k=1.
- Problemes del colom
de la pau
- 1. C.
Com deia l'enunciat aquest és un
problema clàssic. Si dos gats es mengen entre tots
dos dues rates en dos minuts, cada gat triga 2 minuts a
menjar-se una rata. Si hi ha 14 gats, en 14 minuts cadascun
menjarà 7 rates i en total 14·7=98.
- 2. B.
N'hi ha prou amb plantejar l'equació
10000 x = 4/x i trobareu que x=0,02.
- 3. D.
Com que tots els costats del pentàgon son nombres
enters, també ho han de ser els costats del triangle
rectangle retallar. Si mireu els nombres que es donen només
i penseu en les ternes pitagòriques veureu que només
pot ser que la hipotenusa del triangle rectangle sigui 5,
i els catets d'aquest triangle rectangle hauran de ser 3
i 4. Per tant a l'esquerra i a la dreta hi han d'anar dos
nombres que es diferenciïn en 3, i a baix i a dalt
dos nombres que es diferenciïn en 4 (també podria
ser a la inversa, però la conclusió seria
la mateixa)
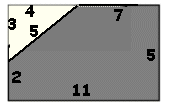
L'àrea buscada és la del rectangle menys la
del triangle retallat: 49.
- 4. A.
Si f(2x)=4x2-20x+24
= (2x)2-10·(2x)+24 la funció
serà f(X)=X2-10X+24. Els valors de X que
compleixen f(X)=3 són 6 i 4. Si posem X = z/2 veurem
que els corresponents valors de z són 12 i 8, que
sumen 20.
- Reptes
- 1. 5
Si pensem em el diagrama d'arbre
que explica l'experiència veurem que el nombre de
casos possibles és N·(N-1). D'aquests, hi
ha N-1 casos favorables (que són les parelles (1,2),
(2,3),... (N-1,N). La probabilitat serà (N-1)/(N·(N-1))
= 1/(N-1). Si aquest valor ha de ser el 20%, és a
dir 1/5, resulta N = 5.
2.
6. Vegeu
una figura que, sense cap càlcul, mostra que si "entra"
al problema el número N, en surt N+1. Es tracta de
dividir el segment BE en cinc parts (exactament igual es
faria si la raó inicial fos un altre nombre enter)
i fer paral·leles al segment DE.

- 3. Resposta:
1. Podeu
obrir una finestra
de la calculadora Wiris i veureu que l'única solució
del sistema és x=4, y=-1, que ens dóna x+3y
= 1.
Els dos darrers
reptes (sobre tot l'últim!) i el problema del "rectangle
retallat" són els que han enganyat més, si
més no en el primer intent. Però ja està
bé que alguns reptes facin pensar una mica, veritat que
sí?
|
|

