Per si voleu dedicar més temps a fer matemŕtiques, teniu tot seguit tres reptes "de propina". Els podeu fer en l'ordre que vulgueu.

Per si us interessa, us podeu descarregar un PDF amb els enunciats

Problema 1 "de propina"

En la corba  que representa la cňnica  x2 + 22x + 593 = y2 només hi ha dos punts (x,y) per als quals les dues coordenades siguin nombres enters positius.  Calcula la suma de les abscisses d'aquests dos punts.
Per a comprovar la resposta de "propina 1"
Problema 2 "de propina"

En el triangle ABC, l'altura AD divideix el costat BC en dos segments de longituds BD = 7 cm i DC = 18 cm.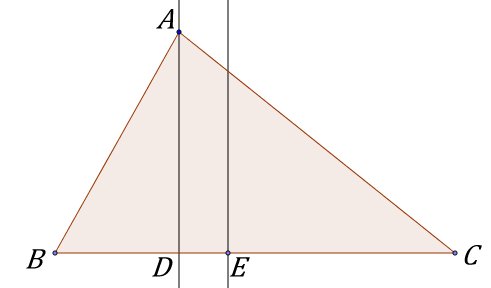

Per un punt E del costat BC fem una paral.lela a l'esmentada altura de manera que divideixi el triangle ABC en dues regions de la mateixa ŕrea. Calculeu la longitud del segment CE.
Problema 3 "de propina"

Tenim tres nombres enters positius,  a, b, c en progressió geomčtrica.
Si restem quatre unitats al tercer terme de la progressió i deixem els dos primers termes sense variació, aleshores els tres nombres queden en progressió aritmčtica.
Si restem una unitat al segon i al tercer terme d'aquesta segona progressió i deixem igual el primer, aleshores els tres nous nombres queden altra vegada en progressió geomčtrica.
Quant sumen els tres termes de la progressió inicial?