|
Problemes a l'esprint per a equips de 3r i 4t d'ESO |
12 i 13 de desembre de 2018Resposta raonada a un dels problemes de propina
| El triangle ABC es rectangle en C. El punt D és el punt mitjà del costat AC . La recta BE és la bisectriu de l'angle en B del triangle. L'àrea del triangle ABC és 144 i la del triangle DBE és 8. Calcula la longitud de la hipotenusa AB i com a resposta envia el quadrat d'aquesta longitud. |  |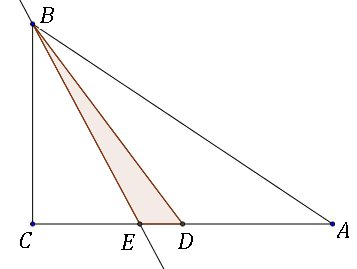
|
Aquest problema és un bon exemple que, en problemes de triangles que es relacionen amb una d eles bisectriu, la ocnsideració d'una recta perpendicular pot se rmolt interessant. |
|
|
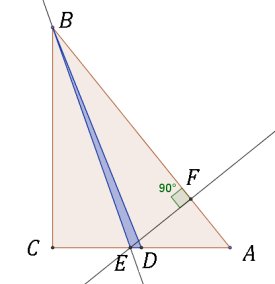
Com que BCD és mig triangle del triangle ABC, aleshores BCD té àrea 72. Com que BED és un triangle que té la mateixa
altura i àrea 8, resulta que "la base" CD ha de ser 9 vegades "la base"
ED
Per tant, si posem ED= x tenim doncs CE = 8x i DA=9x
SI fem per E la perpendicular a la bisectriu, podem raonar que el triangle BCE és igual al triangle BEF .
En el triangle rectangle FED serà el catet EF = 8x i la hipotenusa EA =10 x i, és clar, pel teorema de Pitàgores l'altre catet FA=6x.
Ara bé, si pensem quins són els angles veurem que aquest triangle és semblant al triangle ABC inicial.
Per
tant els catets del triangle donat estan en la relació 6 a 8, posem.los com 6y i
8y. Com que l'àrea és 144 tenim que 6y·8y/2=144 i per tant y =
Com que la hipotenusa mesura 10 y.= 10 , la resposta que s'havia d'enviar (el quadrat de la hipotenusa) és 600. |
 |