Problemes a l'esprint - 29 de gener de 2009

Respostes comentades

Publiquem les solucions oficials dels problemes i, per a atendre la petició d'alguns dels centres participants, adjuntem unes idees per a la solució de cada problema.

• Com s'ha fet en altres ocasions, obrim aquesta pàgina a tothom que vulgui enviar altres propostes per a obtenir la solució.
• En aquesta ocasió es va tenir present la idea d'aquesta activitat i es va considerar la diversitat dels equips dels diversos centres, però amb el benentès que en la majoria dels casos un subgrup fa uns problemes "més fàcils" (els de la branca d'olivera) i un altre subgrup uns altres problemes, a priori "més difícils" (els del colom de la pau) i, en acabat, convé que tots junts pensin els reptes finals entre els quals, per aquesta raó, "n'hi ha d'haver adequats per a tothom". Podeu enviar les vostres opinions sobre aquest tema i també sobre la possibilitat de fer dues convocatòries diferenciades, una per al segon cicle d'ESO i una altra per al batxillerat.
  
  
• Problemes de la branca d'olivera
• 1. 2419. Si S = 25·60/100, 60 = 80·U/100, 80=M ·25/100 i  A= 2009, es calcula i resulta S + U + M + A = 2419
  
• 2. 9. Es pot fer per multiplicacions reiterades per 11 (només cal escriure les dues últimes xifres de cada multiplicació parcial) i es veu que la xifra de les desenes de 11ⁱ segueix la cadència 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, 1, 2, 3 ,... i per això 11²⁰⁰⁹ acaba en 9.
  Però si a algú li agraden més les fórmules pot fer 11²⁰⁰⁹ =(10 + 1)²⁰⁰⁹ i aplicant el binomi de Newton això resulta una suma de molts sumands múltiples de 100 + 2009·10¹·1²⁰⁰⁸ + 1²⁰⁰⁹ que és un número que acaba en 91.
  
• 3. 270. El costat més llarg del rectangle ha de ser el de 20.
  L'altre costat "no retallat" del rectangle ha de ser el de 15 perquè la suma de les longituds dels dos costats del rectangle ha de ser més gran que la suma dels altres tres costats del pentàgon.
  
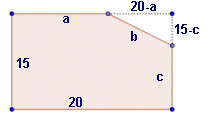
  A partir d'aquí es poden estudiar totes les variacions possibles per assignar a a, b, c els valors 8, 10 i 13 i pensar que en el triangle retallat, de costats 20-a, b, 15-c s'ha de complir el teorema de Pitàgores. Es veu que l'única possibilitat és a = 8, b = 13, c = 10 i així resulta un triangle rectangle de catets 12 i 5 i hipotenusa 13.
  
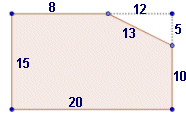
  Després ja només cal calcular l'àrea del rectangle inicial (20·15=300) i restar-li l'àrea del triangle retallat (12·5/2=30) i es veu que l'àrea del pentàgon és 270.
  
• 4. 8,3%. Si volem que 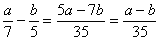, igualant la resposta correcta i la que obtindrà l'Antoni, veiem que s'ha de complir
  
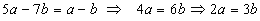
  Com que ha de ser 10 > a > b i a, b nombres enters, s'observa que les úniques possibilitats són a=3, b=2; a=6, b=4 i a=9, b=6.
  Com que per altra banda el nombre de parelles (a,b) que compleixen 10 > a > b i a, b nombres enters és 36, el percentatge d'encerts serà de 100·3/36 = 100/12 que correspon al 8,3%.
  
• 5. 6. Passa el nombre 270 com a volum de l'ortoedre. L'única manera de posar el 270 com a producte de tres nombres enters més petits que 10 és la següent: 270 = 5 · 6 · 9. Vist això la superfície exterior inicial de l'ortoedre és s = 2·(5·6+5·9+6·9). La superfície exterior dels 270 cubets unitaris serà 270·6 de la qual quedarà per pintar 270·6 - s. Com que per pintar s hem necessitat un pot de pintura hemd e fer una divisió i veurem que necessitarem 5 pots i escaig, és a dir que n'haurem de comprar 6.
  
  
• Problemes del colom de la pau
  • 6. 270º. Desplegaments:
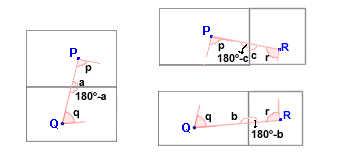
                    Cares on són els punts P, Q, R: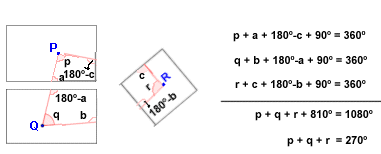
    
  • 7. 6847. Ve d'un altre problema R=2419. Si 2009+2419=4428 nombres tenen de mitjana 4428 és que sumen 4428².
    Els 2419 nombres inicials, com que tenen de mitjana 2419 sumen 2419².
    Per tant els 2009 nombres que hem afegit sumen s = 4428² - 2419² i, doncs, tenen de mitjana s/2009 = 6847.
    
  • 8. Opció per als centres sense alumnes de batxillerat:7/5. (Resultat curiós: la raó de les àrees entre les dues figures és igual a a raó entre els seus perímetres!)
    Si designem com x el costat del triangle inicial el seu perímetre és 3x; el perímetre de l'hexàgon serà 3x - 6.
    
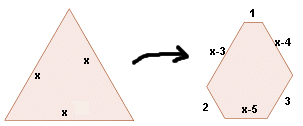
    Si imposem que la raó entre 3x i 3x - 6 sigui 7/5 resulta x = 7.
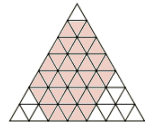
    Tot i que la relació entre les àrees es pot trobar per càlcul tot seguit proposem una solució gràfica, dividint el triangle inicial en 49 triangles equilàters de costat 1, que permet comprovar de seguida que la relació d'àrees és 7/5.
    
    8. Opció general: .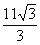
    Si designem com a un dels costats dels rectangles d'àrea coneguda tenim els altres:
    
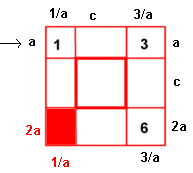
    Si indiquem com c el costat del quadrat centrat i C el costat del quadrat inicial, serà:
    
    
  • 9. Opció per als centres sense alumnes de batxillerat:2/9. Si observem les 36 possibilitats (i, j) on i és, el que marca un dau i j el que marca l'altre, i pensem en els possibles quadrats perfectes que podrem escriure (16, 25, 36, 64) veurem que hi ha 8 casos favorables: { (1,6), (6,1), (2,5), (5,2), (3,6), (6,3), (6,4), (4,6). La probabilitat demanada és doncs 8/36 = 2/9.
    9. Opció general: 20/27.
    Si pensem en els possibilitats per guanyar un jugador, que són: guanyar els dos primers sets, guanyar el primer i el tercer o bé guanyar el segon i el tercer tindrem que la probabilitat demanada és:
    
    

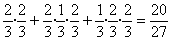
• Reptes
  • 10. 862. Atenent al nombre 7 que ve del problema 10 hem d'estudiar quina és la ma`xima quantitat denombres que podem posar en uns ubconjunt S del conjunt C = {1, 2, 3, …, 2008, 2009} a fi i efecte que entre els nombres seleccionats no n'hi hagi cap parella que sumi un múltiple de 7.
    Si classifiquem els nombres de C segons el residu que donen quan els dividim per 7, en tindrem 287 que donen residu 1, 287 que donen residu 2, ... 287 que són múltiples de 7.
    Si posem un nombre de residu 1 en el subconjunt S no n'hi podem posar cap de residu 6 i recíprocament. Però sí que podem posar tots els d'una classe: en total 287.
    El mateix amb els de residu 2 i els de residu 5: en total 287, perquè cap d'aquests sumat amb els anteriors pot donar un múltiple de 7. I semblantment amb els de residu 3 i residu 4. Tenim 287 candidats més a pertànyer a S.
    I pel que fa als múltiples de 7? Dos no els podrem posar però un múltiple de 7 sí que pot pertànyer a S, que només pot donar per suma un múltiple de 7 amb un altre múltiple de 7.
    Així doncs podem posar 3·287+1 = 862 nombres al subconjunt S.
    
  • 11. 1139. Tot i que també es pot donar una solució explicativa, donem una solució algebraica.
                 
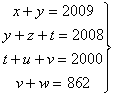
    Sumant la primera i la tercera equació i, a part, la segona i la quarta obtenim
    
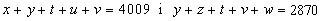
    i si ara restem aquestes dues,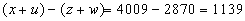
    
  • 12. 4800. Tenim 6 tones = 6000 kg, dels quals el 92%, que són 5520 kg és aigua i, doncs, 480 kg no són aigua. Aquests 480 kg seran, després del transport, el 10% del total del pes que arriba. Per tant el pes del carregament quan arriba a destinació és 4800 kg.