

(no celebrada a Catalunya)
Nivell C

  |
Prova Cangur-1995 (no celebrada a Catalunya) Nivell C |
Menú Cangur-95 
|

| 1. |
Si u ¹ v i les successions (u, a1, a2, v, ...) i (u, b1, b2, v, ...) són progressions aritmètiques, llavors 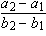 és igual a és igual a
|
|
| 2. |
Per cada terna de nombres reals no nuls, a, b, c, formem el nombre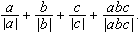 El conjunt de nombres obtinguts és |
|
| 3. |
Quin és el valor del paràmetre p que fa que les equacions |
|
| 4. |
Si x < 0, llavors 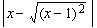 és igual a és igual a
|
|
| 5. | Quines són les dues funcions que tenen els gràfics de la figura?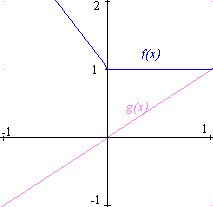
|
|
| 6. |
Si r és positiu i la recta d'equació x + y = r és tangent a la circumferència d'equació x2 + y2 = r, llavors r és igual a |
|
| 7. | Jo vivia a Siracusa fa més o menys 22 segles; vaig calcular l'àrea d'un segment de paràbola i d'altres coses; he demostrat que l'àrea lateral del cilindre circumscrit a una esfera és igual a l'àrea d'aquesta esfera; una certa espiral porta el meu nom; però, per damunt de tot, se sap que vaig dir «Doneu-me un punt de suport, i ...» Qui sóc? |
|
| 8. |
Un trapezi ABCD té costats paral·lels de longituds AB = 40 cm i CD = 16 cm. El punt P està sobre AB de manera que el segment DP divideix el trapezi en dues parts de la mateixa àrea. Calculeu la longitud de AP expressada en centímetres. |
|
| 9. |
Si desenvolupem la potència (2x – 1)1995 i ordenem els termes, obtenim a1995x1995 + a1994x1994 + ··· + a1x + a0. Llavors la suma a1995 + a1994 + ··· + a1 + a0 val |
|
| 10. |
Digueu quina de les funcions indicades a les respostes no està representada a la figura següent:
 |
|

| 11. |
Si 1 + 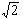 anul·la la funció f(x) = x2 + px + q, amb p, qÎ Z, llavors anul·la la funció f(x) = x2 + px + q, amb p, qÎ Z, llavors p + q val |
|
| 12. |
Si (x, y, z) és una solució del sistema 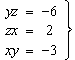 |
|
| 13. | En un triangle ABC, el punt mitjà de BC és M, AB = 4 cm, BC = 6 cm i AM = 5 cm. L'àrea del triangle, expressada en centímetres quadrats, és |
|
| 14. |
Es defineix la successió Sn de terme general 
|
|
| 15. |
Donada la successió (un), definim D1(un) = un+1 – un, i per tot enter k > 1, definim Dk(un) = D1(Dk–1(un)). Si un = n3 + n, llavors, pot ser Dk(un) = 0 per tot n? |
|
| 16. |
Si a és un angle agut i  llavors tan a és llavors tan a és
|
|
| 17. |
Si la funció 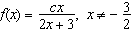 compleix f(f(x)) = x (per a tot x ¹ –3/2), llavors c val |
|
| 18. |
Si c és un nombre real i una de les solucions no positives de x2 – 3x + c = 0 és també una solució de x2 + 3x – c = 0, llavors les solucions de l'equació x2 – 3x + c = 0 són |
|
| 19. | Siguin C1, C2 i C3 tres cordes paral·leles entre elles i al diàmetre d'un semicercle. La distància entre C1 i C2 és la mateixa que entre C2 i C3. Les longituds de les cordes són 20 cm, 16 cm i 8 cm. Encara que a primera vista no ho sembli, pots determinar el radi del cercle que, expressat en centímetres, és |
|
| 20. |
El gràfic de la figura, simètric respecte Oy, representa una funció contínua que és la derivada d'una funció f. Digueu quina de les afirmacions següents és falsa.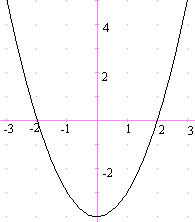 |
|

| 21. | Dues circumferències iguals, de radi 10 cm, són tangents exteriors. Les tangents a la de la dreta es tallen al centre de la de l'esquerra. Busca un valor aproximat de l'àrea de la part acolorida de la figura, i arrodoneix-lo als centímetres quadrats. | 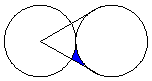
|
|
| 22. |
Si m, n, p, q són nombres reals i considerem les funcions |
|
| 23. |
El cercle K té diàmetre AB. El cercle L és tangent a K i a AB en el centre de K. El cercle 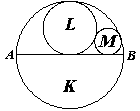
|
| 24. | En una circumferència de radi 6 es dibuixa un sector circular d'angle central agut iagual a a. EL radi de la circumferència circumscrita a aquest sector és |
|
| 25. |
Si (a, b) i (c, d) són dos punts de la recta d'equació y = mx + n, la distància entre ells és |
|
| 26. | A la figura, les rectes AD i AE divideixen en tres parts iguals l'angle A del triangle ABC. Les longituds de BD, DE i EC són, respectivament, 2 cm, 3 cm i 6 cm. Quina és, expressada en centímetres, la longitud del costat més petit del triangle ABC? | 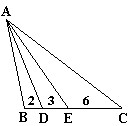
|
|
| 27. | El nombre d'extrems locals de la funció f(x) = 2x – x3 + sin x és |
|
| 28. |
El nombre natural solució de l'equació
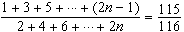
|
|
| 29. |
Si k és un nombre enter i f una funció tal que, per tot nombre real positiu x, compleix 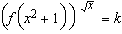 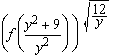 |
|
| 30. | El nombre de solucions reals de l'equació (x2 – 1)3 – 3(x2 – 1)2 + 1 = 0 és |
|