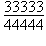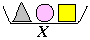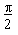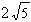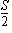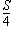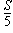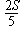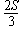|
| 3. | En un cert joc, el director del joc ha de cantar en veu alta i correlativament tots els nombres des de l'1 fins al 100. Els jugadors i les jugadores han d'aplaudir cada vegada que es canta un nombre que sigui múltiple de 3 o que acabi en 3. Si tu has guanyat el joc perquè has aplaudit sempre que calia, quantes vegades has aplaudit? |
|
| 4. | L'1 de juliol, en una població molt al Nord, el sol surt a les 4:53 i es pon a les 21:25. A quina hora serà el migdia local d'aquesta població, si succeeix justament entremig de la sortida i la posta del sol? |
|
| 5. | A la figura, K, L, M i N són els punts mitjans dels costats d'un rectangle ABCD. De manera semblant O, P, R i SN són els punts mitjans dels costats del quadrilàter KLMN. Quina part de la superfície del rectangle ABCD s'ha acolorit? | 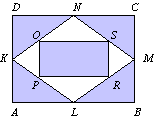 |
|
| 6. |
Les safates P, Q, R estan en ordre creixent dels seus pesos totals.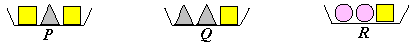
|
|
| 7. | Un Cangur vol anar, saltant, d'un punt B a un altre punt C, que és a 2002 km de B. Ara bé, aquest Cangur és màgic i té la capacitat de fer salts molt llargs, cadascun de 23 quilòmetres. Quants salts necessitarà per sobrepassar el punt C i quants quilòmetres li hauran sobrat? |
|
| 8. |
L'Aina, el Vicent, el Narcís i l'Empar tenen cadascú un sol animal escollit en el conjunt
Quina de les frases següents no és correcta: |
|
| 9. | El dau que veus a la figura no és com els habituals. A la cara inferior, que no es veu a la figura, hi ha el 6; a la cara de l'esquerra, el 4, i a la cara del darrera, el 2. Si mous el dau per veure les 3 cares concurrents en un vèrtex de totes les maneres possibles, quin és el nombre màxim de punts veuràs alhora? |  |
|
| 10. | En una zona de Canadà són oficials l'anglès i el francès. Tothom sap algun dels idiomes, però una part de la població només sap l'anglès, una part només el francès i una part coneix tots dos idiomes. Si llegeixes que el 85% de la població pot parlar l'anglès i el 75% el francès, quin tant per cent de la població parla tots dos idiomes? |
|
| 11. | A la casella superior esquerra d'un engraellat 2002´2002 hi ha situada una fitxa i les altres estan numerades com es pot veure a la figura. En cada moviment, la fitxa es pot moure cap avall o a la dreta a la casella adjacent a aquella on estava. Després d'exactament 2002 moviments, quin nombre marcarà la casella on estarà la fitxa? |  |
|
| 12. | La tripulació d'una caravel·la va salvar d'un naufragi 30 persones. La caravel·la portava provisions suficients per als 60 dies de travessa. Tanmateix, mantenint les mateixes racions, les provisions van allargar només 50 dies. Quantes persones formaven la tripulació de la caravel·la? |
|
| 13. | El nostre Cangur ha dibuixat dues circumferències i tres rectes en un full de paper i ha acolorit tots aquells punts que pertanyen a dos o més dels objectes dibuixats. Quin és el màxim nombre de punts d'intersecció que pot haver acolorit el Cangur? |
|
| 14. | P i Q són els centres de dues circumferències tangents. La línia dels centres, PQ, les talla en els punts A i B. El rectangle ABCD és tangent en el punt T a la circumferència de centre Q. L'àrea del rectangle ABCD és 15. Si dibuixem el triangle PQT, quina serà la seva àrea? | 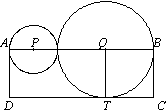
|
|
| 15. | Cinc participants en el nivell 2 del Cangur es pesen per parelles de totes les maneres possibles. Els resultats de les pesades són 90 kg, 92 kg, 93 kg, 94 kg, 95 kg, 96 kg, 97 kg, 98 kg, 100 kg i 101 kg. Si es pesessin conjuntament, quin seria el pes total, expressat en kg? |
|
| 16. | A l'hora de les postres, ha resultat que alguna de les quatre persones que eren a la taula s'havia menjat abans d'hora una part del pastís. El pare diu: "jo no he estat!"; la mare diu: "jo tampoc!"; la filla diu: "ha estat el meu germà!"; el fill diu: "No! ha estat el pare!". Només tres han dit la veritat. Qui s'havia mejat el pastís? |
|
| 17. | En una caixa hi havia 17 caramels que s'han menjat entre Aina, Biel i Carles. L'Aina diu: «jo he menjat més caramels que ningú». Quin és el mínim nombre de caramels que ha d'haver menjat Aina per poder estar segura de la seva afirmació? |
|
| 18. |
Si 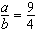 i i 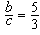 llavors llavors 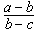 és igual a és igual a
|
|
| 19. | Vols posar monedes en un engraellat de 2´9, de manera que en cada casella o bé hi hagi una moneda o bé tingui un costat en comú amb una altra casella on hi ha una moneda. Quin és el nombre mínim de monedes que necessitaràs? |  |
|
| 20. | D'entre tots els nombres enters, n, divisibles per 21 i per 9, quants divisors positius té el nombre n que té menys divisors enters positius? |
|
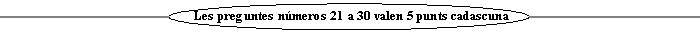
| 21. | El senyor Cangur triga 90 segons a pujar caminant per unes escales mecàniques quan no funcionen. Quan les mateixes escales funcionen i el senyor Cangur es queda quiet, triga 60 segons a pujar el mateix trajecte. Quants segons trigaria a pujar si caminés alhora que les escales funcionen? |
|
| 22. | Un joc de taula té peces en forma de triangle equilàter dividides en tres parts iguals, que s'acoloreixen amb tres colors triats entre tres colors que anomenarem 1, 2, 3, 4 i 5, de manera que no es repeteixi cap color en una fitxa. Es poden fer rotacions a les fitxes per col·locar-les al tauler, però no se'ls pot donar la volta. Quantes peces diferents pot tenir aquest joc? |
|
|
Exemple: Vegeu tres peces que fan servir els colors 1, 2 i 3. Les peces (*) i (**) que es poden obtenir per rotació l'una de l'altra, són la mateixa. En canvi la peça (***) és diferent a les anteriors: s'obté mitjançant una simetria. | 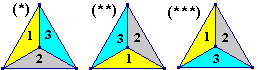 |
| 23. | El mateix mes d'un cert any tres diumenges han estat en un dia amb nombre parell. En quin dia de la setmana ha caigut el dia 20 d'aquell mes? |
|
| 24. | En una població de rates, el 25% són blanques i el 75%, negres. De les rates blanques, el 50% tenen la cua llarga i, de les negres l'hi tenen el 20%. Sabem que hi ha 99 rates amb la cua llarga. Quantes rates hi ha a la població? |
|
| 25. | L'esfera d'un rellotge com el de la figura s'ha trencat en tres trossos de manera que la suma dels nombres de cada part és la mateixa. Sabent que cap de les dues línies de trencament separa els dígits de cap dels nombres de dues xifres, quina de les frases següents podem assegurar que és certa? |  |
|
| 26. | La llista 1, x2, ..., xn – 1, 1000 és la més llarga que es pot formar de manera que acabi en el número 1000 i que cada terme xk, k > 2, sigui la suma de tots els que el precedeixen. Quant val x2? |
|
| 27. | Un cub de costat 5 està format enganxant petits cubs de costat 1. En traiem tres fileres de cubs, les que estan acolorides a la figura. Tot seguit submergim el cos que resulta en un pot de pintura. Quants cubs tenen només una cara pintada? |  |
|
| 28. | Considereu el conjunt de tots els nombres de quatre xifres formats amb els dígits 1, 2, 3 i 4, sense repeticions. Quant sumen tots els nombres d'aquest conjunt? |
|
| 29. |
A la figura, els triangles ABC i DEC són iguals, i CB = CE = 4. | 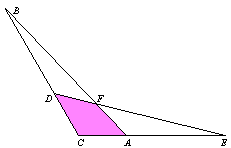 |
| 30. |
A partir d'un full de paper quadrat formem un pentàgon com es mostra a les figures. Primer de tot es fan dos doblecs al full de manera que els vèrtexs B i D es porten sobre la diagonal AC. Tot seguit en la figura que ha resultat es fa un doblec fins que el vèrtex C es superpon al vèrtex A. El valor de l'angle assenyalat amb el signe ? és:
 |
|



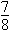 B =
B = 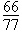 C =
C = 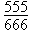 D =
D = 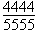 E =
E =