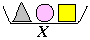Cangur 2002 de la SCM.
Nivell 1		 Portada
1. 2002 és un nombre cap-i-cua: es llegeix igual d'esquerra a dreta que de dreta a esquerra. Quin dels nombres següents no té aquesta propietat?
  1. 1991
  2. 2323
  3. 2112
  4. 2222
  5. 2442
2. Tot seguit pots veure la silueta d'un castell a l'horitzó:
 
Quina de les peces següents no pot pertànyer a la silueta?
  1. A
  2. B
  3. C
  4. D
  5. E
3. La mare i el pare Cangur tenen 3 petites canguretes. Cada cangureta té dos germans cangurets. De quants membres consta la família Cangur?
  1. 11
  2. 9
  3. 8
  4. 7
  5. 5
4. Quins nombres han de substituir els signes ? en les caselles ombrejades (la superior i la inferior, respectivament)?
  1. 2 i 14
  2. 2 i 30
  3. 3 i 221
  4. 4 i 14
  5. 4 i 30
5. Aquest any, l'endemà del dia del meu aniversari vaig poder dir amb tota correcció
«Demà passat serà dijous».
En quin dia de la setmana va caure el meu aniversari enguany?
  1. dilluns
  2. dimarts
  3. dimecres
  4. dijous
  5. divendres
6. En quin dels següents collarets formats per petits cors hi ha dos terços dels cors de color fosc?
  1. A
  2. B
  3. C
  4. D
  5. E

 
7. Quina de les expressions següents té el valor més gran?
  1. 10 ´ 0,001 ´ 100
  2. 0,01 ¸ 100
  3. 100 ¸ 0,01
  4. 10000 ´ 100 ¸ 10
  5. 0,1 ´ 0,01 ´ 10000
8. Quants angles de mides diferents es poden veure en la zona ombrejada de la figura?
  1. 4
  2. 6
  3. 8
  4. 10
  5. 11
 
9. L'àrea d'un rectangle és igual a 1. Si unim els punts mitjans de dos costats adjacents es forma un triangle i un pentàgon. Quant és l'àrea del triangle?
  1. 1/3
  2. 1/4
  3. 2/5
  4. 3/8
  5. 1/8
10. Les safates P, Q, R estan en ordre creixent dels seus pesos totals.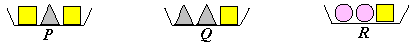
Si volem col·locar-hi la safata X de manera que es mantingui l'ordenació dels pesos de les safates, on hem de posar-la?
  1. P < X < Q
  2. Q < X < R
  3. X < P
  4. R < X
  5. X = una de les altres safates
 
11. Els polígons I, II, III i IV són quadrats. Els perímetres dels quadrats I i II són, respectivament, 16 cm i 24 cm. Calcula, en cm, el perímetre del quadrat IV.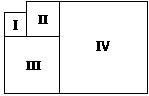
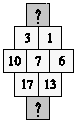
  1. 56
  2. 60
  3. 64
  4. 72
  5. 80
12. Una abella es mou d'una cel·la a una altra del rusc seguint una determinada regla. A quina cel·la anirà en el proper moviment?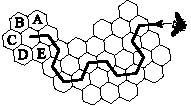
  1. A
  2. B
  3. C
  4. D
  5. E
13. Una sala mesura 4 m ´ 5 m i fa 3 m d'alt. Si s'ha d'augmentar el seu volum en 60 m3 aixecant-ne el sostre, quants metres l'haurem de sobreelevar?
  1. 1
  2. 2
  3. 3
  4. 4
  5. 6
14. El mag Antoni ha posat en el seu barret màgic 14 ratolins grisos, 8 de blancs i 6 de negres. Quin és el mínim nombre de ratolins que ha d'agafar amb els ulls tapats per tenir l'absoluta certesa que té, com a mínim, un ratolí de cada color?
  1. 23
  2. 21
  3. 15
  4. 7
  5. 4
15. L'Aina, el Vicent, el Narcís i l'Empar tenen cadascú un sol animal escollit en el conjunt
{un gat, un peix, un canari, un gos}.
El Vicent té un animal pelut; l'Empar té un animal de quatre potes; el Narcís té un ocell; a l'Aina i al Vicent no els agraden els gats.
Quina de les frases següents no és correcta:
  1. L'Empar té un gos
  2. El Narcís té un canari
  3. L'Aina té un peix
  4. L'Empar té un gat
  5. El Vicent té un gos
16. La Carlota ha afegit 3 g de sal a 17 g d'aigua. Quin és el percentatge de sal en la solució que ha obtingut?
  1. 20 %
  2. 17 %
  3. 16 %
  4. 15 %
  5. 3 %
17. Considera el conjunt de nombres de tres xifres escrits amb tres dígits diferents (i, per tant, compresos entre 100 i 999). Calcula la diferència entre el nombre més gran i el més petit d'aquest conjunt.
  1. 899
  2. 885
  3. 800
  4. 100
  5. 888
18. Un virus en el disc dur del meu ordinador se m'està menjant l'espai del disc. Durant el primer dia destrueix l/2 de l'espai total del disc, durant el segon dia 1/3 de l'espai que quedava i el tercer dia es menja 1/4 de l'espai que havia deixat el dia abans. Quina part del disc original encara està intacta?
  1. 1/4
  2. 1/6
  3. 1/12
  4. 1/24
  5. No queda res intacte
19. Si prens un nombre de tres xifres, fas la suma d'aquestes xifres i, tot seguit, del nombre resultant tornes a sumar les xifres, quin és el valor més gran que pots obtenir?
  1. 9
  2. 10
  3. 11
  4. 12
  5. 18
20. Cinc participants en el nivell 1 del Cangur es pesen per parelles de totes les maneres possibles. Els resultats de les pesades són 90 kg, 92 kg, 93 kg, 94 kg, 95 kg, 96 kg, 97 kg, 98 kg, 100 kg i 101 kg. Si es pesessin conjuntament, quin seria el pes total, expressat en kg?
  1. 225
  2. 230
  3. 239
  4. 240
  5. 250
21. En un cert joc, el director del joc ha de cantar en veu alta i correlativament tots els nombres des de l'1 fins al 100. Els jugadors i les jugadores han d'aplaudir cada vegada que es canta un nombre que sigui múltiple de 3 o que acabi en 3. Si tu has guanyat perquè has aplaudit sempre que calia, quantes vegades has aplaudit?
  1. 30
  2. 33
  3. 36
  4. 39
  5. 43
22. Les longituds dels costats del rectangle que es pot veure a la figura són a i b. Quina és la suma de les longituds de tots els segments dibuixats a l'interior del rectangle, amb el benentès que tots ells són paral·lels a algun dels costats del rectangle?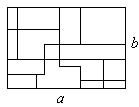
  1. 3(a + b)
  2. 3a + b
  3. 3a + 2b
  4. 2a + 3b
  5. cal conèixer els valors numèrics d'a i de b.
23. Un ciclista puja un trajecte de muntanya a la velocitat de 12 km/h i tot seguit baixa pel mateix camí a 20 km/h. La diferència entre el temps que ha trigat per fer la pujada i el temps del descens ha estat de 16 minuts. Quina és la longitud de la pujada?
  1. 8 km
  2. 10 km
  3. 12 km
  4. 14 km
  5. Falten dades
24. 2 gats, que mengen contínuament i igual tots dos, es mengen 2 rates en dues hores. Si tenim 10 gats que mengen rates al mateix ritme que els anteriors, quantes rates es menjaran en 10 hores?
  1. 10
  2. 20
  3. 50
  4. 100
  5. 200
25. A la dreta es poden veure quatre figures acolorides formades a partir de quadrats iguals on s'han marcat els punts mitjans dels costats. Quina de les relacions següents és correcta?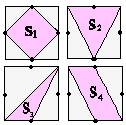
  1. S3 < S4 < S1 = S2
  2. S3 < S1 = S2 = S4
  3. S3 < S1 = S4 < S2
  4. S3 < S4 < S1 < S2
  5. S4 < S3 < S1 < S2
26. Volem col·locar els nombres enters de l'1 al 7 cada un en un dels cercles de la figura de la dreta de manera que s'obtingui la mateixa suma en cadascuna de les files de tres cercles alineats. Quina de les afirmacions següents és correcta?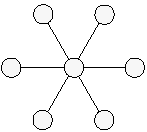
  1. És impossible
  2. Ho podem fer de manera única
  3. Hi ha 2 nombres diferents que poden ocupar el lloc central
  4. Hi ha 3 nombres diferents que poden ocupar el lloc central
  5. Tots els 7 nombres poden ocupar el lloc central
27. Les cares d'un cub estan acolorides, cadascuna d'elles amb un color diferent. El Pere, la Sònia i la Bet es miren el cub per separat i diuen quines són les tres cares que veuen sense girar-lo. El Pere diu: «Blau, blanc, groc»; la Sònia: «Negre, blau, vermell » i la Bet: «Verd, negre, blanc». De quin color està pintada la cara oposada a la de color blanc?
  1. vermell
  2. blau
  3. negre
  4. verd
  5. groc
28. El nostre Cangur ha dibuixat dues circumferències i tres rectes en un full de paper i ha acolorit tots aquells punts que pertanyen a dos o més dels objectes dibuixats. Quin és el màxim nombre de punts d'intersecció que pot haver acolorit el Cangur?
  1. 18
  2. 17
  3. 16
  4. 15
  5. 14
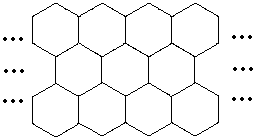
29. Amb peces com aquesta 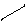, que pesen 200 g cadascuna, construïm un enreixat format per hexàgons, disposats en 3 files anàlogament al que mostra la figura de la dreta. L'enreixat s'amplia fins a un total de 32 hexàgons. Quin és el pes total de l'enreixat?
  1. 24,6 kg
  2. 24,4 kg
  3. 26,4 kg
  4. 30,4 kg
  5. 28,6 kg
30. En un torneig de basquet participen 32 equips. En cada fase de la competició els equips es reparteixen en grups de 4 equips que juguen tots contra tots una vegada. Els dos millors equips de cada grup de 4 es classifiquen per la fase següent i els altres dos queden eliminats. Després de la darrera fase, quan ja només quedava en competició un grup de 4 equips, els dos primers juguen la final del campionat a un sol partit. Quants partits s'hauran jugat en total en aquest campionat?
  1. 49
  2. 89
  3. 91
  4. 97
  5. 181